Project page: http://rncarpio.github.com/linterp
What is linterp?
linterp is a C++ header-only library for N-dimensional linear interpolation on a rectangular grid, similar to Matlab's interpn command. For interpolation on unstructured data, take a look at delaunay_linterp. Arbitrary dimensions are supported, but the number of dimensions must be specified as a template parameter at compile time. Two algorithms for computing the interpolated value are available:
- Multilinear: This uses the values at the 2^N vertices of the N-dimensional hypercube containing the point. In two dimensions, this is equivalent to bilinear interpolation; in 3 dimensions, trilinear, etc. Each interpolation step is O(2^N).
- Simplicial: This uses the values at the N+1 vertices of the N-dimensional simplex containing the point. Each hypercube of the rectangular grid is split into simplices; the simplex containing a point
xis determined by sorting the coordinates ofx. Each interpolation step is O(N log N). Compared to the multilinear algorithm, this becomes much faster in higher dimensions, at the cost of decreased accuracy (since less neighboring points are used to control the interpolated value).
The number type is user-specified as a template parameter. The underlying data may be shared or copied. If a reference-counting scheme is used for the memory containing the underlying data, an optional reference-counting type may be passed as a template parameter.
Requires the boost.multi_array library.
For a description of the two interpolation algorithms, see:
- Weiser & Zarantonello (1988), "A Note on Piecewise Linear and Multilinear Table Interpolation in Many Dimensions", Mathematics of Computation 50 (181), p. 189-196
- Davies (1996), "Multidimensional Triangulation and Interpolation for Reinforcement Learning", Proceedings of Neural Information Processing Systems 1996
C++ interface
Here is an example in C++:
#include <ctime>
#include "linterp.h"
// return an evenly spaced 1-d grid of doubles.
std::vector<double> linspace(double first, double last, int len) {
std::vector<double> result(len);
double step = (last-first) / (len - 1);
for (int i=0; i<len; i++) { result[i] = first + i*step; }
return result;
}
// the function to interpolate.
double fn (double x1, double x2) { return sin(x1 + x2); }
int main (int argc, char **argv) {
const int length = 10;
// construct the grid in each dimension.
// note that we will pass in a sequence of iterators pointing to the beginning of each grid
std::vector<double> grid1 = linspace(0.0, 3.0, length);
std::vector<double> grid2 = linspace(0.0, 3.0, length);
std::vector< std::vector<double>::iterator > grid_iter_list;
grid_iter_list.push_back(grid1.begin());
grid_iter_list.push_back(grid2.begin());
// the size of the grid in each dimension
array<int,2> grid_sizes;
grid_sizes[0] = length;
grid_sizes[1] = length;
// total number of elements
int num_elements = grid_sizes[0] * grid_sizes[1];
// fill in the values of f(x) at the gridpoints.
// we will pass in a contiguous sequence, values are assumed to be laid out C-style
std::vector<double> f_values(num_elements);
for (int i=0; i<grid_sizes[0]; i++) {
for (int j=0; j<grid_sizes[1]; j++) {
f_values[i*grid_sizes[0] + j] = fn(grid1[i], grid2[j]);
}
}
// construct the interpolator. the last two arguments are pointers to the underlying data
InterpMultilinear<2, double> interp_ML(grid_iter_list.begin(), grid_sizes.begin(), f_values.data(), f_values.data() + num_elements);
// interpolate one value
array<double,2> args = {1.5, 1.5};
printf("%f, %f -> %f\n", args[0], args[1], interp_ML.interp(args.begin()));
// interpolate multiple values: create sequences for each coordinate
std::vector<double> interp_grid = linspace(0.0, 3.0, length*10);
int num_interp_elements = interp_grid.size() * interp_grid.size();
std::vector<double> interp_x1(num_interp_elements);
std::vector<double> interp_x2(num_interp_elements);
for (int i=0; i<interp_grid.size(); i++) {
for (int j=0; j<interp_grid.size(); j++) {
interp_x1[i*interp_grid.size() + j] = interp_grid[i];
interp_x2[i*interp_grid.size() + j] = interp_grid[j];
}
}
std::vector<double> result(num_interp_elements);
// pass in a sequence of iterators, one for each coordinate
std::vector< std::vector<double>::iterator > interp_x_list;
interp_x_list.push_back(interp_x1.begin());
interp_x_list.push_back(interp_x2.begin());
// interpolate a sequence of values
clock_t t1, t2;
t1 = clock();
interp_ML.interp_vec(num_interp_elements, interp_x_list.begin(), interp_x_list.end(), result.begin());
t2 = clock();
printf("multilinear: %d interpolations, %d clocks, %f sec\n", num_interp_elements, (t2-t1), ((double)(t2 - t1)) / CLOCKS_PER_SEC);
// calculate the squared errors
std::vector<double> true_f_vals(num_interp_elements);
double SSE = 0.0;
for (int i=0; i<num_interp_elements; i++) {
true_f_vals[i] = fn(interp_x1[i], interp_x2[i]);
double diff = true_f_vals[i] - result[i];
SSE += diff*diff;
}
printf("sum of squared errors: %f\n", SSE);
return 0;
}
produces
1.500000, 1.500000 -> 0.137236
multilinear: 10000 interpolations, 1 clocks, 0.001000 sec
sum of squared errors: 1.812171
Python interface
A Python interface is provided, using Andreas Klöckner's pyublas library. Scipy's griddata command provides similar functionality and can interpolate unstructured data, but is slower and can handle fewer points.
An example:
import _linterp_python as _linterp
x = scipy.linspace(-3, 3, 10)
xi = scipy.linspace(-3.5, 3.5, 30)
y = scipy.sin(x)
f = _linterp.Interp_1_ML([x], y)
yi = f.interp_vec([xi])
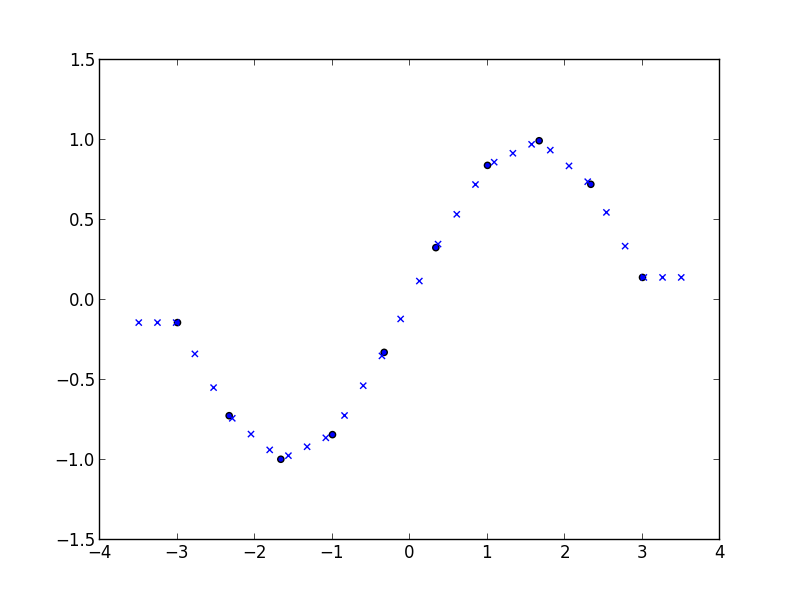
scatter(x, y)
scatter(xi, yi, marker='x')
produces
Matlab interface
A Matlab interface is provided. To compile it with mex, supply the appropriate include directory for the Boost headers:
mex -IC:/boost/boost_1_49_0 linterp_matlab.cpp
Example:
grid_min = -2;
grid_max = 2;
grid_size = 10;
xi_min = grid_min * 1.2;
xi_max = grid_max * 1.2;
xi_size = grid_size * 10;
% function to interpolate
sin_sum_1 = @(x) sin(x);
sin_sum_2 = @(x1, x2) sin(x1+x2);
% max error, error sum of squares
err_ss = @(true_y, y) [max(abs(y-true_y)), sum((y-true_y) .* (y-true_y))];
% 1D
grid_1 = linspace(grid_min, grid_max, grid_size); % original grid
xi_grid_1 = linspace(xi_min, xi_max, xi_size); % grid of points to interpolate on
f = sin_sum_1(grid_1); % f evaluated on original grid
xi_mesh_1 = xi_grid_1;
true_y = sin_sum_1(xi_mesh_1);
% matlab's interp1
yi_1 = interp1(grid_1,f,xi_mesh_1); % interpolated value
not_nans = not(isnan(yi_1));
disp('interp1: max err, err SS');
disp(err_ss(true_y(not_nans), yi_1(not_nans)));
figure('Name', 'interp1');
plot(grid_1,f,'o', xi_grid_1,yi_1,'x')
% linterp
yi_2 = linterp_matlab(grid_1,f,xi_grid_1); % interpolated value
disp('linterp: max err, err SS');
disp(err_ss(true_y(not_nans), yi_2(not_nans)));
figure('Name', 'linterp 1d');
plot(grid_1,f,'o', xi_grid_1,yi_2,'x')
% 2D
grid_1 = linspace(grid_min, grid_max, grid_size); % original grid
grid_2 = linspace(grid_min, grid_max, grid_size);
xi_grid_1 = linspace(xi_min, xi_max, xi_size); % grid of points to interpolate on
xi_grid_2 = linspace(xi_min, xi_max, xi_size);
[grid_mesh_1, grid_mesh_2] = ndgrid(grid_1, grid_2);
[xi_mesh_1, xi_mesh_2] = ndgrid(xi_grid_1, xi_grid_2);
f = sin_sum_2(grid_mesh_1, grid_mesh_2); % f evaluated on original grid
true_y = sin_sum_2(xi_mesh_1, xi_mesh_2);
figure('Name', 'true function');
mesh(grid_1, grid_2, f);
% matlab's griddata 2d
disp('griddata:');
tic;
yi_1 = griddata(grid_mesh_1, grid_mesh_2, f, xi_mesh_1, xi_mesh_2); % interpolated value
toc;
not_nans = not(isnan(yi_1));
disp(err_ss(true_y(not_nans), yi_1(not_nans)));
figure('Name', 'griddata 2d');
mesh(xi_grid_1, xi_grid_2, yi_1);
err = yi_1 - true_y;
figure('Name', 'griddata 2d errors');
mesh(xi_grid_1, xi_grid_2, err);
% linterp 2d
disp('linterp 2d:');
tic;
yi_2 = reshape(linterp_matlab(grid_1, grid_2, f, xi_mesh_1, xi_mesh_2), size(true_y)); % interpolated value
toc;
disp(err_ss(true_y(not_nans), yi_2(not_nans)));
figure('Name', 'linterp 2d');
mesh(xi_grid_1, xi_grid_2, yi_2);
err = yi_2 - true_y;
err(isnan(yi_1)) = NaN;
figure('Name', 'linterp 2d errors');
mesh(xi_grid_1, xi_grid_2, err);
produces
interp1: max err, err SS
0.0240 0.0159
linterp: max err, err SS
0.0240 0.0159
griddata:
Elapsed time is 0.574771 seconds.
0.0926 4.8782
linterp 2d:
Elapsed time is 0.001489 seconds.
0.0474 3.7872
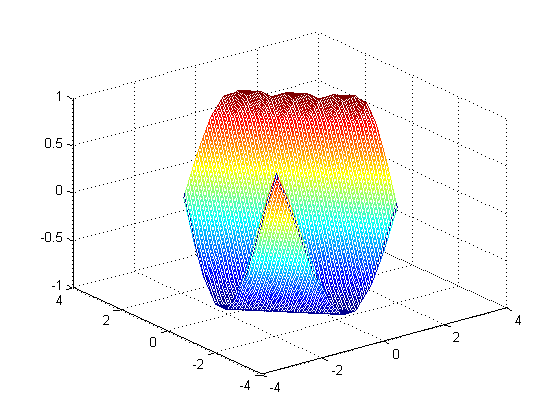
output of griddata:
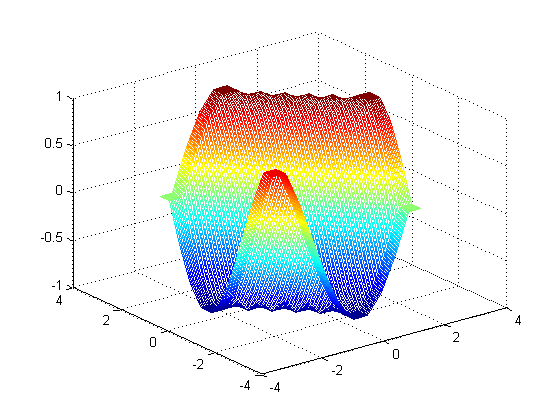
 output of
output of linterp:
License
Permission to use, copy, modify, distribute and sell this software and its documentation for any purpose is hereby granted without fee, provided that the above copyright notice appear in all copies and that both that copyright notice and this permission notice appear in supporting documentation. The authors make no representations about the suitability of this software for any purpose. It is provided "as is" without express or implied warranty.